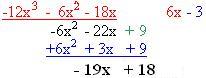Essa semana nos (Aline e Yuri) resolvemos explicar passo a passo da resolução da divisão de polinômios, pois muitos não entenderam. Na sala de aula nos decidimos isso e juntos cada um pesquisou uma parte o Yuri sobre o que é um polinômio e a Aline sobre o exercício resolvido. Vamos explicar primeiro o que é um polinômio e depois um exercício resolvido de divisão de polinômios passo a passo.
Polinômio é uma expressão formada de vários monômios. (Poli = muitos)
P(x) = P(x) = Hans + an-1xn-1 + an-2xn-2 + ... + a2x² + a1x +a0
ao , a1 , ... , an são os coeficientes
n é um número natural denominado grau do polinômio
x é a variável do polinômio.
a0 é o termo indepedente da variável x.
Agora vamos com o exemplo da divisão de polinômios com o método da chave:
Onde: A(x) /B(x)
R(x) Q(x)
A(x) é o Dividendo
B(x) é o Divisor
Q(x) é o quociente
R(x) é o Resto.
Exemplo:
Para dividir o polinômio: A(x) = 4x3 + x4 + 9 + 4x2 pelo polinômio B(x) = x2 + x – 1.
adotamos um procedimento análogo(igual) ao algoritmo(processo) usado na aritmética.
(1º Passo)
Escreve-se os polinômios dados na ordem decrescente de seus expoentes, e completa-se o com termos de coeficiente zero.
A(x) = x4 + 4x3 + 4x2 + 0x + 9 e B(x) = x2 + x – 1.
(2º Passo)
Dividimos o termo de maior grau do dividendo pelo termo de maior grau do divisor. Obtemos, desta forma, o primeiro termo do quociente.
A seguir, multiplica-se o termo obtido pelo divisor e subtrai-se esse produto do dividendo.
x4 + 4x3 + 4x2 + 0x + 9 /x2 + x – 1
-x4 – x3 + x2 x²
3x3 + 5x2 + 0x + 9
(3º Passo)
Caso a diferença obtida tenha grau maior ou igual ao do divisor, ela passa a ser um novo dividendo. Repete-se o processo a partir do 2º passo. Veja:
x4 + 4x3 + 4x2 + 0x + 9 /x2 + x – 1
-x4 – x3 + x2 x² + 3x + 2
3x3 + 5x2 + 0x + 9
-3x3 – 3x2 + 3x
2x2 + 3x + 9
-2x2 – 2x + 2
x + 11
Obtemos: Q(x) = x2 + 3x + 2 e R(x) = x + 11